Consistent hashing, a guide & Go library

Consistent hashing is deceptively simple yet very powerful, but I didn’t quite understand what it was till I sat down and worked it out for myself. Before I tell you about consistent hashing, you need to understand the problem we’re trying to solve:

How to determine which server to store and retrieve keys in a distributed network? Requirements are: all nodes get relatively equal number of keys, be able to add and remove nodes such as fewest number of keys are moved around.

Let’s assume couple things: There are four servers in the network: Chico, Harpo, Groucho and Zeppo. All four servers are identical, but have no knowledge of each other.

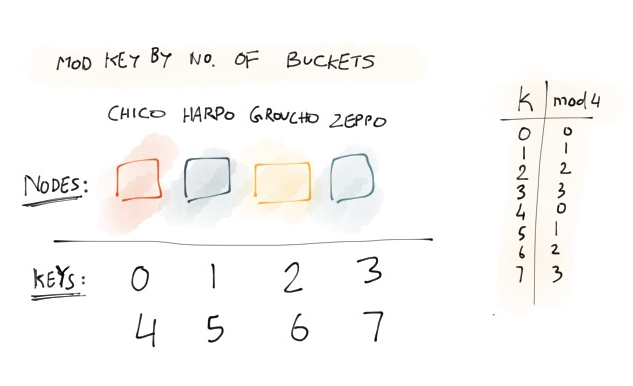
To keep things simple in this example the keys are incrementing integers. Usually you run the key against a checksum to return a number. Once you have that number, you can take the modulo of that number against the number of nodes. This works surprisingly when the network is stable, ie no nodes are leaving or joining the network.

But, what happens if a node, ie Harpo goes down, like he’s always prone to doing. Then we’ve a big problem. Using the same hash function, we get the same result, but apply modulo operation we get different results than before, since the number of nodes is reduced by one.

Note how nearly all the keys from all nodes need to be remapped as well. This make no sense, why should the keys that in servers that are functioning properly have to be remapped?! Do you share my exclamation yet? Well now we’ve arrived at the need for consistent hashing.

Consistent hashing is a special kind of hashing such that when a hash table is resized and consistent hashing is used, only K/n keys need to be remapped on average, where K is the number of keys, and n is the number of slots.
Source: https://en.wikipedia.org/wiki/Consistent_hashing

If we had used consistent hashing above, then only the keys from Harpo need to be moved around. Usually this is when most posts include a picture of an unit circle and explain it in terms of that. Let’s do it:

For time being ignore how the nodes were placed onto the unit circle. Instead of applying modulo function on the hash of the key, let’s map the hash onto the unit circle. (I know this is hand waving, but we’ll get to the implementation soon enough). To determine which node the key maps to, we simply go clockwise till we find a node. So for key 1, Harpo is the node it should be stored and retrieved from.

So what if Harpo goes down? You’ll need to get and retrieve key 1 from a different node, however note how rest of the key mappings haven’t changed. The only keys that have changed are the ones that used to live in Harpo node. Voila! This works if you add new nodes as well. Say you add Gummo to the network. You don’t need to change the residence of existing keys.

Consistent hashing also covers situations where nodes differ in size. What you do is create virtual nodes and make them onto the unit circle. Depending on the hash function you chose, the virtual nodes can be made to place randomly on the unit circle. For nodes with more capacity, you should add more virtual nodes. This way when a node goes down, the keys are distributed evenly across other nodes, not just to the next one.

Implementation

Let’s go the extra mile here and implement a consistent hash library in Go. I didn’t quite understand it till I found a good implementation and put print statements everywhere and changed the code. This implementation is heavily inspired by stathat’s implementation. The original paper calls for using trees for implementation, however I prefer the way stathat did it.

Let’s define a bird’s eye view:

// Initializes new distribute network of nodes or a ring.
func NewRing() *Ring

// Adds node to the ring.
func (r *Ring) AddNode(id string)

// Removes node from the ring if it exists, else returns
// ErrNodeNotFound.
func (r *Ring) RemoveNode(id string) error

// Gets node which is mapped to the key. Return value is identifer
// of the node given in `AddNode`.
func (r *Ring) Get(key string) string

We’ll use crc32 for generating a checksum of the key. Explaining what crc32 does and how it does it is beyond scope of this blog post. Just know that given an input, it returns a 32 uint. Input in this case is the ipaddress of the node.

The gist of it is we use an array to hold the result of node id checksums. For each key we run the checksum and determine the position the key should be added and return the node closet to that. If it’s out of bounds of array, we return the first node.

First, let’s define Ring, which is just a collection of Node

package consistenthash

// Ring is a network of distributed nodes.
type Ring struct {
  Nodes Nodes
}

// Nodes is an array of nodes.
type Nodes []Node

// Node is a single entity in a ring.
type Node struct {
 Id     string
 HashId uint32
}

Next, let’s write the initializer functions for Ring and Node:

package consistenthash

func NewRing() *Ring {
  return &Ring{Nodes : Nodes{}}
}

func NewNode(id string) *Node{
  return &Node{
    Id        : id,
    hashedKey : crc32.Checksum([]byte(id)),
  }
}

Now we’re finally ready to fill in AddNode:

func (r *Ring) AddNode(id string) {
  node := NewNode(id)
  r.Nodes = append(r.Nodes, node)

  sort.Sort(r.Nodes)
}

Why sort.Sort? This goes back to the unit circle. How exactly do you implement an unit circle? One way is to have an array with the last item pointing to the first item in the entry. We can use a linked list for this, but you’ll see soon enough why that’s unnecessary.

If you run what we’ve so far, Go compiler will throw something at you because Nodes doesn’t implement sort.Sort interface. That’s pretty easy to do:

package consistenthash

func (n Nodes) Len() int           { return len(n) }
func (n Nodes) Less(i, j int) bool { return n[i].HashId < n[j].HashId }
func (n Nodes) Swap(i, j int)      { n[i], n[j] = n[j], n[i] }

Let’s continue with Get which is the point of this all:

func (r *Ring) Get(key string) string {
  searchfn := func(i int) bool {
    return r.Nodes[i].HashId >= crc32.Checksum([]byte(key))
  }

  i := sort.Search(r.Nodes.Len(), searchfn)
  if i >= r.Nodes.Len() {
    i = 0
  }

  return r.Nodes[i].Id
}

sort.Search uses binary search to find exitense of node in array. If it doesn’t exist, it returns the place where the node should be added if we were to add it. If the node cheksum is greater than the last node, then we add it to the first node. And that’s it.

If you want to check the rest of the code, it’s open sourced here, along with some tests.

Remember how it told you in the beginning consistent hashing was deceptively simple, yet powerful? Believe me yet? You should know consistent hashing was first introduce in a paper by Akamai who know a thing or two about distributed systems. An improved version of consistent hashing is used in the Chord algorithm which is a distributed hash table. (earlier version said Chord is behind Amazon dynamodb, which is incorrect.)

I’m still in the process of reading and understanding chord, not to mention implementing it myself, will do a blog post here once that’s done. I had a lot of fun learning about consistent hashing, implementing it, not to mention writing this blog post, hope you learned a thing or do. If you find an error or think something can be said better, you can tweet me @sent-hil.