Logits, Softmax and Temperature in LLMs
My notes on Logits and Softmax.
Logits and Softmax
- When LLM processes an input, it generates set of numerical scores (logits) for each possible token in its vocabulary.
- These logits aren’t probability yet, they can be positive or negative and don’t sum to \(1\).
- To turn logics into probabilities, model applies softmax function which normalizes them into a probability distribution over all possible tokens.
- Higer logits correspond to higher probabilities after softmax.
- Softmax function converts vector of real numbers (logits) into probabilitiy distribution.
- Given a vector of logits \(z = [z_1, z_2, ..., z_n]\), softmax function transforms each \(z_i\) into probability. \(\ \sigma(z_i) = \Large \frac{e^{z_i}}{\sum_{j = 1}^{n}{e^{z_j}}}\)
- \(e^{z_i}\) - exponentiates each logic, ensuring all values are positive.
- The denominator sums over all exponentiated logics, normalizing them into a probability distribution.
- Sum of all outputs is always \(1\), making it a valid probability distribution.
From the graph below, you can see the behavior of \(exp(\frac{z_j}{T})\) as \(T\) changes.
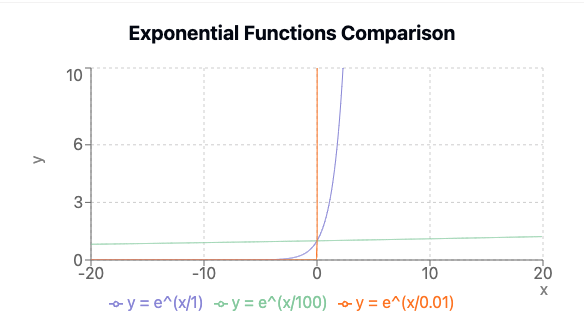
Temperature in LLMs
- We can think of temperature as generalization of softmax. We can apply a scaling factor \(T\) to softmax function.
- When \(T = 1\), result is exactly same as standard softmax function.
- While setting \(T = 1\) implies determinism, since matrix calculations are done as floating point arithmetic, this can lead to rounding errors which can cascade through calculations.
- Floating point operations are not associative, ie \((a + b) + c \neq a + (b +c)\).
- If two tokens have same probability, models need a mechanism to break the tie, which could be non deterministic.